问题
解答题
据市场调查，某种商品一年内每件出厂价在6千元的基础上，按月呈f（x）=Asin（ωx+φ）+B的模型波动（x为月份），已知3月份达到最高价8千元，7月份价格最低为4千元，该商品每件的售价为g（x）（x为月份），且满足g（x）=f（x-2）+2。
（1）分别写出该商品每件的出厂价函数f（x）、售价函数g（x）的解析式；
（2）问哪几个月能盈利？
答案
解：（1）f（x）=Asin（ωx+φ）+B，
由题意可得， A=2，B=6，ω=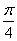
，φ=-
，
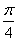所以f（x）=2sin（
x-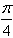
）+6（1≤x≤12，x为正整数）
g（x）=2sin（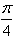
x-
π）+8（1≤x≤12，x为正整数）。
（2）由g（x）>f（x），得sin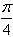
x＜
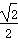
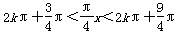，k∈Z
∴8k+3＜x＜8k+9，k∈Z，
∵1≤x≤12，k∈Z，
∴k=0时，3＜x＜9，
∴x=4，5，6，7，8；
k=1时，11＜x＜17，∴x=12
∴x=4，5，6，7，8，12，
故4，5，6，7，8，12月份能盈利。