问题
解答题
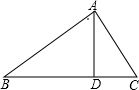
在△ABC中，AD⊥BC，BD＞CD，求证：AB＞AC．
答案
证明：∵BD＞CD，延长BC至E，使DE=DB，连接AE．
∵AD⊥BC，
∴AD是BE的中垂线，
∴AE=AB，∠B=∠E，
∵∠ACE＞∠B，
∴∠ACE＞∠E，
∴AE＞AC，
∴AB＞AC．
搜题请搜索小程序“爱下问搜题”
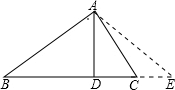
在△ABC中，AD⊥BC，BD＞CD，求证：AB＞AC．
证明：∵BD＞CD，延长BC至E，使DE=DB，连接AE．
∵AD⊥BC，
∴AD是BE的中垂线，
∴AE=AB，∠B=∠E，
∵∠ACE＞∠B，
∴∠ACE＞∠E，
∴AE＞AC，
∴AB＞AC．