问题
解答题
已知向量m=（2cos2x，sinx），n=（1，2cosx）。
（1）若m⊥n，且0＜x＜π，试求x的值；
（2）设f（x）=m·n，试求f（x）的对称轴方程、对称中心、单调递增区间。
答案
解：（1）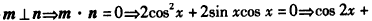
∵
∴
∴
∴
。
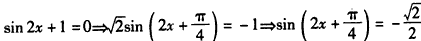
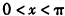
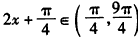
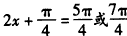
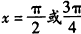（2）
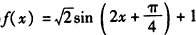
令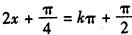
可得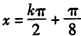
∴对称轴方程为
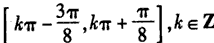
令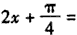
kπ
可得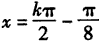
∴对称中心坐标为
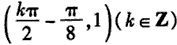
令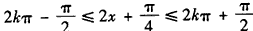
可得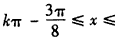
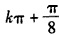
∴f（x）的单调递增区间为
。
搜题请搜索小程序“爱下问搜题”
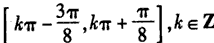已知向量m=（2cos2x，sinx），n=（1，2cosx）。
（1）若m⊥n，且0＜x＜π，试求x的值；
（2）设f（x）=m·n，试求f（x）的对称轴方程、对称中心、单调递增区间。
解：（1）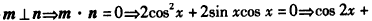
∵
∴
∴
∴。
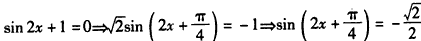
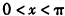
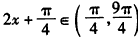
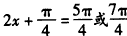
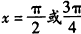（2）
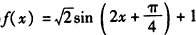
令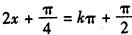
可得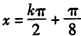
∴对称轴方程为
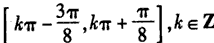
令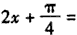kπ
可得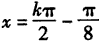
∴对称中心坐标为
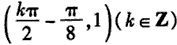
令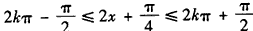
可得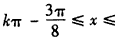
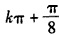
∴f（x）的单调递增区间为
。
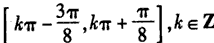