问题
解答题
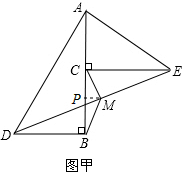
已知：△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=90°．如图甲，连接DE，设M为DE的中点．
（1）说明：MB=MC；
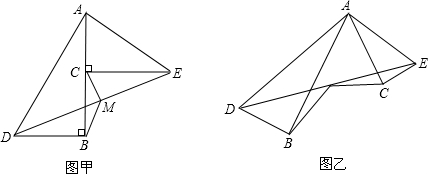
（2）设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图乙的位置，试问：MB=MC是否还能成立？并证明其结论．
答案
证明：（1）作点M作MP⊥AB于点P，
∵∠ABD=∠ACE=90°．
∴MP∥CE∥BD．
∵M为DE的中点，
∴CP=BP，
∴MP是BC的中垂线，
∴MB=MC；
（2）MB=MC成立．
取AD、AE的中点F、G，连接BF、MF、MG、CG显然线段MG、MF都是△ADE的中位线，
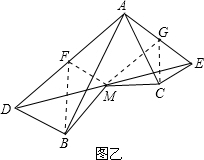∴四边形MFAG是平行四边形，MG=
AD，MF=1 2
AE，1 2
∴∠MFA=∠AGM，
又∵∠DBA=∠ACE=90°，
∴Rt△斜边中线BF=
AD=MG，1 2
CG=
AE=MF，1 2
∵∠DAB=∠CAE，
∴∠BDA=∠CEA，
∴∠BFA=2∠BDA=2∠CEA=∠CGA，
∴∠BFM=∠BFA-∠MFA=∠CGA-∠AGM=∠MGC，
∴△BFM≌△MGC，
∴MB=MC．
