AC=BD；∠B=∠C

题目分析：①过D作DM∥AC得到平行四边形ACMD和△DMB，证△ABC≌△DCB得到∠DBC=∠ACB=∠M，根据等角对等边即可得出AC=BD．②首先过D作DE∥AB，把梯形转化成平行四边形和等腰三角形，根据性质即可得出答案．

①证明：过D作DM∥AC交BC的延长线于M，

∵AD∥CB，DM∥AC，

∴四边形ACMD是平行四边形，

∴AC=DM，∠ACB=∠M，

∵AD∥BC，AB=DC，

∴∠ABC=∠DCB，

∵BC=BC，AB=DC，

∴△ABC≌△DCB，

∴∠DBC=∠ACB，

∴∠DBC=∠M，

∴DB=DM，

即：AC=BD；

②证明：过D作DE∥AB交BC于E，

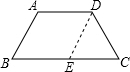
∵AD∥BC，DE∥AB，                                                             

∴四边形ABED是平行四边形，

AB=DE，∠B=∠DEC，

∵AB=CD，

∴∠DEC=∠C，

∴∠B=∠C．

点评：解此题的关键是作辅助线把梯形转化成平行四边形和等腰三角形．