问题
解答题
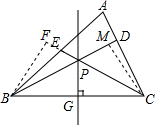
如图所示,在△ABC中,PG为BC边的垂直平分线.且∠PBC=
 |
答案
证明:证明:作BF⊥CE于F点,CM⊥BD于M点,
则∠PFB=∠PMC=90°.
∵PG是BC的垂直平分线,
∴PB=PC.
在△PBF和△PCM中,
,∠PFB=∠PMC ∠BPF=∠CPM PB=PC
∴△PBF≌△PCM(AAS),
∴BF=CM;
∵PB=PC,
∴∠PBC=∠PCB=
∠BPE.1 2
∵∠PBC=
∠A,1 2
∴∠A=∠BPE.
∴∠EPD+∠BPE=∠EPD+∠A=180°,
∴∠AEP+∠ADP=180°.
又∠AEP=∠BEF,∠ADP+∠CDM=180°,
∴∠BEF=∠CDM.
在△BEF和△CDM中,
,∠BEF=∠CDM ∠BFE=∠CMD BF=CM
∴△BEF≌△CDM(AAS).
∴BE=CD.