问题
解答题
在△ABC中,已知(a+b+c)(a+c﹣b)=3ac.
(1)求角B的度数;
(2)求2cos2A+cos(A﹣C)的取值范围.
答案
解:(1)由(a+b+c)(a+c﹣b)=3ac得
a2+c2﹣b2=ac
由余弦定理得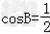
所以角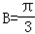 .
.
(2)由(1)知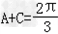
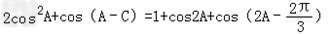
=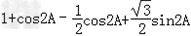
=
由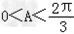 得
得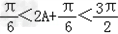
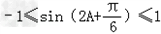
所以2cos2A+cos(A﹣C)的取值范围为[0,2].
