问题
解答题
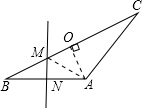
如图,在△ABC中,AB=AC,∠A=150°,AB的垂直平分线MN分别交BC、AB于点M、N,若BM=3,求BC的长.
答案
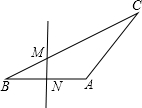
连接AM,过点A作AO⊥BC于点O.(1分)
∵AB=AC,∴∠B=∠C(等边对等角),又∠BAC=150°,
∴∠B=∠C=15°(2分)
∵MN是AB的垂直平分线,
∴AM=BM=3.(线段垂直平分线上的点到这条线段两个端点的距离相等)(3分)
∴∠MAB=∠B=15°(等边对等角),
∴∠AMO=∠B+∠MAB=30°.(4分)
又∵AO⊥BC,
∴OA=
AM=1 2
(直角三角形中,30°的角所对直角边等于斜边一半)(5分)3 2
在Rt△AOM中,由勾股定理,得MO=
=AM2-OA2
=32-(
)23 2
.(7分)3 3 2
∴BO=BM+MO=3+
(8分)3 3 2
∵AB=AC,∴△ABC是等腰三角形,而AO⊥BC,
∴BO=OC.(等腰三角形底边上的高、底边上的中线互相重合)(9分)
则BC=2BO=6+3
.(10分)3