由已知得f（x）是偶函数，且在区间[-

π

2

，0]上递减，在[0，

π

2

]上递增，

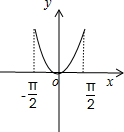
作出函数的草图，如图所示：

由图象可知，f（x₁）＞f（x₂）⇔|x₁|＞|x₂|，即x₁²＞x₂²．故①符合，②不符合；

由x₁＞x₂，且

x1+x2

2

＞0，知x₁＞0，

若x₂＞0，则显然f（x₁）＞f（x₂）成立；

若x₂＜0，由x₁+x₂＞0，得x₁＞-x₂，

即|x₁|＞|x₂|，有f（x₁）＞f（x₂）成立，故③符合；

故答案为：①③．