问题
解答题
某简谐运动的图象对应的函数解析式为:y=
(1)指出此简谐运动的周期、振幅、频率、相位和初相; (2)利用“五点法”作出函数在一个周期(闭区间)上的简图; (3)说明它是由函数y=sinx的图象经过哪些变换而得到的. |
答案
(1)∵y=
sin(2x-3
),π 4
∴周期为π;振幅
;频率为2
;相位为2x-1 π
;初相为-π 4
;(每空1分)π 4
(2)
| x |
|
|
|
|
| ||||||||||
2x-
| 0 |
| π |
| 2π | ||||||||||
sin(2x-
| 0 | 1 | 0 | -1 | 0 | ||||||||||
| y | 0 |
| 0 | -
| 0 |
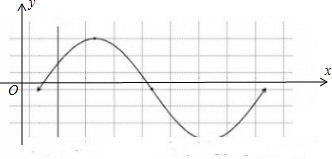
(3)①先将函数y=sinx的图象上的点纵坐标不变横坐标缩短至原来的一半 得到函数y=sin2的图象;②再将函数y=sin2x的图象右移
个单位得到函数y=sin(2x-π 8
)的图象;③最后再将函数y=sin(2x-π 4
)的图象上的点横坐标不变纵坐标扩大至原来的π 4
倍得到函数y=3
sin(2x-3
)的图象.(每空1分)π 4
