问题
解答题
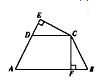
如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB,垂足为F,∠A=∠B。
(1)写出图中相等的线段;(已知的相等线段除外)
(2)选择(1)中你所写出的一组相等线段,说明它们相等的理由;
(3)你还能得到其他结论吗?并说明理由。
答案
解:(1)相等的线段有CE=CF,DE=BF,AE=AF;
(2)CE=CF,理由如下:
∵AB∥CD,
∴∠A=∠EDC,
又∵∠A=∠B,
∴∠B=∠EDC,
∵CE⊥AD,CF⊥AB,
∴∠E=∠CFB,
在△DEC和△BFC中,
∠E =∠CFB,∠EDC=∠B,CD=CB,
∴△DEC≌△BFC(AAS),
∴CE= CF,DE=BF;
(3)还能得到的结论是点C在∠EAB的角平分线上,理由如下:
∵CE⊥AD,CF⊥AB,CE=CF,
∴点C在∠EAB的角平分线上。
