问题
解答题
已知O为坐标原点,
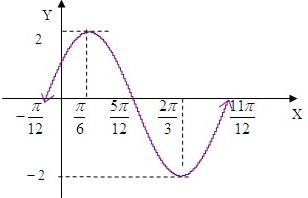
(1)求y关于x的函数关系式f(x); (2)若f(x)的最大值为2,求a的值; (3)利用(2)的结论,用“五点法”作出函数f(x)在长度为一个周期的闭区间上的简图,并指出其单调区间. |
答案
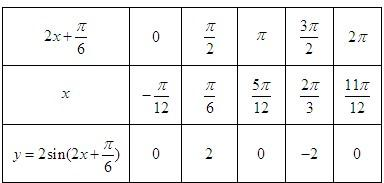
(1)∵
=(2cos2x,1),OA
=(1,OB
sin2x+a)3
∴y=
•OA
=2cos2x+OB
sin2x+a3
(2)由(1)得y=2cos2x+
sin2x+a3
=1+cos2x+
sin2x+a3
=cos2x+
sin2x+a+13
=2(
cos2x+1 2
sin2x)+a+13 2
=2(sin
cos2x+cosπ 6
sin2x)+a+1π 6
=2sin(2x+
)+a+1π 6
当sin(2x+
)=1时,ymax=2+a+1=3+aπ 6
又∵ymax=2
∴3+a=2
∴a=-1
(3)由(2)得,y=2sin(2x+
)π 6
增区间是:[-
+kπ,π 3
+kπ](k∈Z),π 6
减区间是:[
+kπ,π 6
+kπ](k∈Z).2π 3
