问题
解答题
已知动圆C经过坐标原点O,且圆心C在直线l:2x+y=4上.
(1)求半径最小时的圆C的方程;
(2)求证:动圆C恒过一个异于点O的定点.
答案
(1)因为圆心C在直线l:2x+y=4上,
所以设圆心的坐标为(a,4-2a).
又因为动圆C经过坐标原点O,
所以动圆的半径r=
,所以半径r的最小值为5(a-
)2+8 5 16 5
.4 5 5
并且此时圆的方程为:(x-
)2-(y-8 5
)2=4 5
.16 5
(2)设定点坐标(x0,y0),因为圆的方程为:(x-a)2+[y-(4-2a)]2=a2+(4-2a)2
所以x02-2ax0+y02-2(4-2a)y0=0,
即a(4y0-2x0)+(x02+y02-8y0)=0,
因为当a为变量时,x0,y0却能使该等式恒成立,
所以只可能4y0-2x0=0且x02+y02-8y0=0
即解方程组可得:y0=
,x0=8 5
或者y0=0,x0=0(舍去)16 5
所以圆C恒过一定点(
,16 5
).8 5

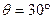 ,导轨上端接一阻值为R=0.5
,导轨上端接一阻值为R=0.5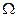 的电阻,其余电阻不计,轨道所在空间有垂直轨道平面的匀强磁场,磁感应强度B=1T,如图所示。有一不计电阻、质量为m=0.5kg的金属棒ab,放在导轨最上端且与导轨垂直。当金属棒ab由静止开始自由下滑到底端脱离轨道的过程中,电阻R上产生的热量为Q=1J,g=10m/s2,则:
的电阻,其余电阻不计,轨道所在空间有垂直轨道平面的匀强磁场,磁感应强度B=1T,如图所示。有一不计电阻、质量为m=0.5kg的金属棒ab,放在导轨最上端且与导轨垂直。当金属棒ab由静止开始自由下滑到底端脱离轨道的过程中,电阻R上产生的热量为Q=1J,g=10m/s2,则: