问题
解答题
求通过原点且与两直线l1:x+2y－9=0,l2:2x－y+2=0相切的圆的 方程.
答案
圆方程为(x－2)2+(y－1)2=5或(x－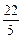
)2+(y+
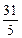)2=
.
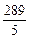∵圆与l1、l2相切，故圆心的轨迹在l1与l2的夹角平分线上.
∵k1=－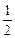
,k2=2,k1·k2=－1,
∴l1⊥l2.
设l1与l2的夹角平分线为l,其斜率为k,故l与l2夹角为45°.
∴|
|=1.
∴k=－3或k=
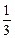(舍去).
l:3x+y－7=0,设圆心(a,b)，则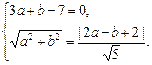
解得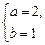
或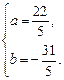
故圆方程为(x－2)2+(y－1)2=5或(x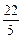－)2+(y+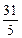)2=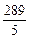.