问题
证明题
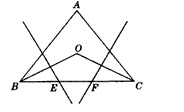
如图所示,在等边三角形ABC中,∠B,∠C的平分线交于点O,OB和OC的垂直平分线交BC于E,F。
求证:BE=EF=FC。
答案
证明:如图所示,连接OE,OF,
因为△ABC为等边三角形,
所以∠ABC=∠ACB=60°,
又因为∠B,∠C的平分线交于点O,
所以∠OBE=∠OCF=30°,
因为OB,OC的垂直平分线分别交BC于E,F,
所以BE=OE,OF=CF,
所以∠BOE=∠OBE=30°,∠COF=∠OCF=30°,
所以∠OEF=∠OFE=60°,
所以OE=OF=EF,
所以BE=EF=FC。

