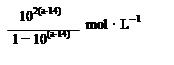问题
选择题
已知函数f(x)=x2+x+
|
答案
∵f(x)=x2+x+
,m x
∴f′(x)=2x+1-
=m x2
;2x3+x2-m x2
设g(x)=2x3+x2-m,∵g′(x)=6x2+2x,
当x∈[1,+∞)时,g′(x)>0,
∴g(x)是增函数,∴g(x)min=g(1)=3-m;
∴f′(x)在x∈[1,+∞)时,有f′(x)min=g(x)min=3-m≥0,f(x)是增函数,
解得m≤3,
∴m的取值范围是{m|m≤3};
故选:A