根据函数单调性的定义,证明函数f (x)=-x3+1在(-∞,+∞)上是减函数.
证明见解析.
本小题考查函数单调性的概念,不等式的证明,以及逻辑推理能力.满分10分.
证法一:在(-∞,+∞)上任取x1,x2且x1<x2 ——1分
则f (x2) -f (x1) =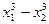 = (x1-x2) (
= (x1-x2) (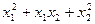 ) ——3分
) ——3分
∵ x1<x2,∴ x1-x2<0. ——4分
当x1x2<0时,有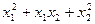 = (x1+x2) 2-x1x2>0; ——6分
= (x1+x2) 2-x1x2>0; ——6分
当x1x2≥0时,有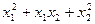 >0;
>0;
∴f (x2)-f (x1)= (x1-x2)(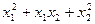 )<0. ——8分
)<0. ——8分
即 f (x2) < f (x1),所以,函数f(x)=-x3+1在(-∞,+∞)上是减函数. ——10分
证法二:在(-∞,+∞)上任取x1,x2,且x1<x2, ——1分
则f (x2)-f (x1)=x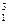 -x
-x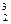 = (x1-x2) (
= (x1-x2) (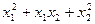 ). ——3分
). ——3分
∵x1<x2,∴x1-x2<0. ——4分
∵x1,x2不同时为零,∴x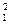 +x
+x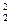 >0.
>0.
又∵x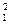 +x
+x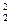 >
>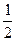 (x
(x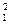 +x
+x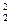 )≥|x1x2|≥-x1x2。∴
)≥|x1x2|≥-x1x2。∴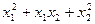 >0,
>0,
∴ f (x2)-f (x1) = (x1-x2) (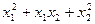 )<0. ——8分
)<0. ——8分
即f (x2) < f (x1).所以,函数f (x)=-x3+1在(-∞,+∞)上是减函数. ——10分
