问题
解答题
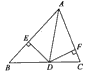
如图,在△ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积是45cm2。求DE的长。
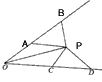
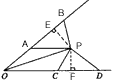
变式:如图AB=CD,△PAB的面积与△PCD的面积相等,求证:PO平分∠BOD。
答案
解:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF(角平分线性质),
又∵S△ABC=S△ABD+S△ADC,
∴45=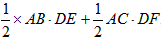 ,
,
即45=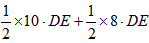 ,
,
∴DE=5cm;
变式:过点P作PE⊥AB于E,PF⊥CD于F,如图
又∵PE⊥OB于E,PF⊥OD于F(由作法可得),
∴OP平分∠BOD(到角的两边距离相等的点在这个角的平分线上)。
选择题
