问题
解答题
定义在R上的偶函数f(x)满足:f(0)=5,x>0时,f(x)=x+
(1)求x<0时,f(x)的解析式; (2)求证:函数f(x)在区间(0,2)上递减,(2,+∞)上递增; (3)当x∈[-1,t]时,函数f(x)的取值范围是[5,+∞),求实数t的取值范围. |
答案
(1)x<0时,f(x)=f(-x)=-x-
;(4分)4 x
(2)任取x1,x2∈(0,2)且x1<x2,
∵f(x1)-f(x2)=(x1-x2)(x1x2-4) x1x2
而x1-x2<0,0<x1•x2<4,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(0,2)上递减;
再任取x1,x2∈(2,+∞)且x1<x2同理可得:
函数f(x)在区间(2,+∞)上递增.
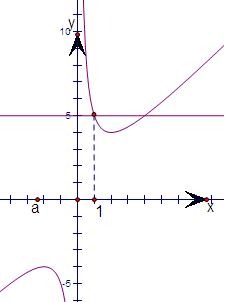
(3)利用y=f(x)的图象,如图,
函数f(x)的取值范围是[5,+∞),易知t∈[0,1].(4分)