问题
解答题
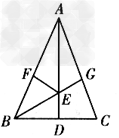
如图，在等腰三角形ABC中，AB =AC，AD是BC边上的中线，∠ABC的平分线BG交AD于点E，EF ⊥AB，垂足为F
求证：EF=ED.
答案
证明：∵AB=AC，AD是BC边上的中线，
∴AD ⊥BC，
∵BG平分∠ABC，EF⊥AB，
∴EF= ED．
搜题请搜索小程序“爱下问搜题”
如图，在等腰三角形ABC中，AB =AC，AD是BC边上的中线，∠ABC的平分线BG交AD于点E，EF ⊥AB，垂足为F
求证：EF=ED.
证明：∵AB=AC，AD是BC边上的中线，
∴AD ⊥BC，
∵BG平分∠ABC，EF⊥AB，
∴EF= ED．