问题
选择题
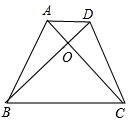
在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是【 】
A.∠BDC =∠BCD
B.∠ABC =∠DAB
C.∠ADB =∠DAC
D.∠AOB =∠BOC
答案
答案:C
题目分析:根据等腰梯形的判定,逐一作出判断:
A.由∠BDC =∠BCD只能判断△BCD是等腰三角形,而不能判断梯形ABCD是等腰梯形;
B.由∠ABC =∠DAB和AD∥BC,可得∠ABC =∠DAB=900,是直角梯形,而不能判断梯形ABCD是等腰梯形;
C.由∠ADB =∠DAC,可得AO=OD,由AD∥BC,可得∠ADB =∠DBC,∠DAC =∠ACB,从而得到∠DBC =∠ACB,所以OB=OC,因此AC=DB,根据对角线相等的梯形是等腰梯形可判定梯形ABCD是等腰梯形;
D.由∠AOB =∠BOC只能判断梯形ABCD的对角线互相垂直,而不能判断梯形ABCD是等腰梯形。
故选C。
