搜题请搜索小程序“爱下问搜题”
问题 填空题
我们把形如y=
b
|x|-a
(a＞0，b＞0)的函数称为“莫言函数”，并把其与y轴的交点关于原点的对称点称为“莫言点”，以“莫言点”为圆心，凡是与“莫言函数”图象有公共点的圆，皆称之为“莫言圆”．当a=1，b=1时，在所有的“莫言圆”中，面积的最小值______．
答案

当a=1且b=1时，函数“莫言函数”为y=

1
|x|-1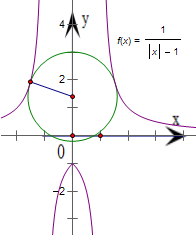

图象与y轴交于（0，-1）点，则“莫言点”坐标为（0，1）．

令“莫言圆”的标准方程为x2+（y-1）2=r2，

令“莫言圆”与函数y=

1
|x|-1
图象的左右两支相切，

则可得切点坐标为（

1+
5
2
，
1+
5
2
）和（-
1+
5
2
，
1+
5
2
），

此时“莫言圆”的半径r=

(
1+
5
2
)2+(
1+
5
2
)2
=
3
；

令“莫言圆”与函数y=

1
|x|-1
图象的下支相切，此时切点坐标为（0，-1）．

此时“莫言圆”的半径r=2；

故所有的“莫言圆”中，面积的最小值为3π．

故答案为：3π．

完形填空
完形填空。
     Jenny and Bruce are good friends. They    1    from Canada. They speak English. They can speak a
little Chinese.They    2    to play with their dolls. Jenny likes English very much. Bruce likes math. They
    3    in Beijing, China now. The weather in Biejing is very good in October. They    4    to school
five days a week (周). They like to play games (游戏)    5    Thursdays. They    6    go to school on Saturdays
or Sundays. They have two Chinese friends.    7    names are Li Ming and Liu Dan. They are    8    the
same class. They like their school. They like China. They say,"The    9   people (人民) are very kind (友好).
The food is good,   10   ."
( )1.A. come     
( )2.A. can     
( )3.A. do     
( )4.A. goes   
( )5.A. at     
( )6.A. do     
( )7.A. His     
( )8.A. to      
( )9.A. Chinese 
( )10.A. much 		B. is    
B. are    
B. are     
B. go      
B. in    
B. don't
B. Their       
B. in       
B. China   
B. very  		C. live       
C. be         
C. don't    
C. going     
C. on        
C. doesn't   
C. They        
C. of       
C. China's  
C. nice     		D. aren't     
D. like          
D. be          
D. are going   
D. for            
D. aren't                     
D. Her          
D. for           
D. Chinese's   
D. too          
查看答案
问答题 简答题

便携式硫化氢检测仪的使用
查看答案