问题
解答题
如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,请你参考这个作全等三角形的方法,解答下列问题:
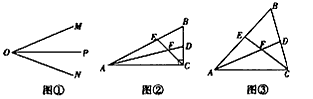
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请你判断并写出FE与FDP之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
答案
解:(1)FE与F之间的数量关系为FE=FD;
(2)(1)中的结论FE=FD仍然成立,理由如下:
在AC上截取AG=AE,连接FG,因为∠1=∠2,AF为公共边,可证△AEF≌△AGF,
所以∠AFE=∠AFG,FE=FG,
由∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
可得∠2+∠3=60°,
所以∠AFE=∠CFD=∠AFG=60°,
所以∠CFG=180°-∠2-∠3-∠AFG=60°,
由∠3=∠4及FC为公共边,
可得△CFG≌△CFD,
所以FG=FD,
所以FE=FD。
