(本小题满分12分)已知函数f(x)=x2-1(x≥1)的图象是C1,函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数;
(3)设A、B是曲线C2上任意不同两点,证明:直线AB与直线y=x必相交.
(1)g(x)= 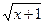 ,M={x|x≥0};(2)略;(3)略
,M={x|x≥0};(2)略;(3)略
解:(1)由y=x2-1(x≥1),得y≥0,且x=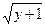 ,
,
∴f-1(x)=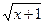 (x≥0),
(x≥0),
即C2:g(x)= 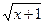 ,M={x|x≥0}. 4分
,M={x|x≥0}. 4分
(2)对任意的x1,x2∈M,且x1≠x2,则有x1-x2≠0,x1≥0,x2≥0.
∴|g(x1)-g(x2)|=|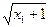 -
-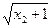 |=
|=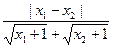 <
<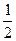 |x1-x2|.
|x1-x2|.
∴y=g(x)为利普希茨Ⅰ类函数,其中a=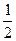 . 8分
. 8分
(3)设A(x1,y1),B(x2,y2)是曲线C2上不同两点,x1,x2∈M,且x1≠x2.
由(2)知|kAB|=|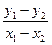 |=
|=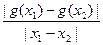 <
<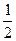 <1.
<1.
∴直线AB的斜率kAB≠1.
又∵直线y=x的斜率为1,∴直线AB与直线y=x必相交. 12分
