问题
证明题
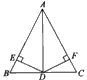
如图，AD是△ABC的中线，DE⊥AB于E点，DF⊥AC于F点，且BE=CF。求证：AD平分∠BAC。
答案
证明：在Rt△DEB和Rt△DFC中，BE=CF，DB=DC，
∴Rt△DEB≌Rt△DFC（HL），
∴DE=DF，
又∵DE⊥AB，DF⊥AC，
∴AD平分∠BAC（到角的两边距离相等的点在这个角的平分线上）。
搜题请搜索小程序“爱下问搜题”
如图，AD是△ABC的中线，DE⊥AB于E点，DF⊥AC于F点，且BE=CF。求证：AD平分∠BAC。
证明：在Rt△DEB和Rt△DFC中，BE=CF，DB=DC，
∴Rt△DEB≌Rt△DFC（HL），
∴DE=DF，
又∵DE⊥AB，DF⊥AC，
∴AD平分∠BAC（到角的两边距离相等的点在这个角的平分线上）。