问题
填空题
与直线l:x+y-2=0和曲线x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是 .
答案
(x-2)2+(y-2)2=2
【思路点拨】数形结合得最小圆的圆心一定在过x2+y2-12x-12y+54=0的圆心与直线x+y-2=0垂直的垂线段上.
解:∵圆A:(x-6)2+(y-6) 2=18,
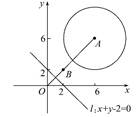
∴A(6,6),半径r1=3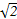
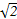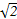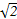,且OA⊥l,A到l的距离为5,显然所求圆B的直径2r2=2,即r2=,又OB=OA-r1-r2=2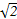,由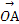
与x轴正半轴成45°角,∴B(2,2),∴方程为(x-2)2+(y-2)2=2.