问题
填空题
任意四边形ABCD中，点E、F、G、H分别是AD、BC、BD、AC的中点，当四边形ABCD满足条件 时，四边形EGFH是菱形．（填一个使结论成立的条件）
答案
AB=CD．
题目分析：E、G分别是AD，BD的中点，那么EG就是三角形ADB的中位线，同理，HF是三角形ABC的中位线，因此EG、HF同时平行且相等于AB，因此EG∥HF且EG=HF．因此四边形EHFG是平行四边形，E、H是AD，AC的中点，那么EH=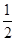
CD，要想证明EHFG是菱形，那么就需证明EG=EH，那么就需要AB、CD满足AB=CD的条件．
需添加条件AB=CD．
试题解析：需添加条件AB=CD．
∵点E，G分别是AD，BD的中点，
∴EG∥AB，且EG=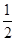AB同理HF∥AB，且HF=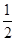AB，
∴EG∥HF，EG=HF．
∴四边形EGFH是平行四边形．
∵EG=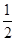AB，
又可同理证得EH=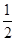CD，
∵AB=CD，
∴EG=EH，
∴四边形EGFH是菱形．
故答案为：AB=CD．
考点: 1.菱形的判定；2.三角形中位线定理．