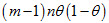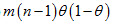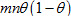问题
解答题
| 解方程 (1)y2-3y=0 (2)x2+
(3)-t2+5t+6=0 (4)9(x-1)2=(2x+1)2. |
答案
(1)因式分解得:y(y-3)=0,
可得y=0或y-3=0,
解得:y1=0,y2=3;
(2)方程整理得:x2+x+
=0,即(x+1 4
)2=0,1 2
解得:x1=x2=-
;1 2
(3)方程变形得:t2-5t-6=0,
分解因式得:(t-6)(t+1)=0,
可得t-6=0或t+1=0,
解得:t1=6,t2=-1;
(4)方程移项得:9(x-1)2-(2x+1)2=0,
分解因式得:[3(x-1)+(2x+1)][3(x-1)-(2x+1)]=0,
即(5x-2)(x-4)=0,
可得5x-2=0或x-4=0,
解得:x1=
,x2=4.2 5

 ()
()