问题
解答题
设函数f(x)＝ax－(1＋a2)x2，其中a>0，区间I＝{x|f(x)>0}．
(1)求I的长度(注：区间(α，β)的长度定义为β－α)；
(2)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I的长度的最小值．
答案
（1）
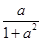（2）
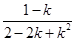
(1)令f(x)＝x[a－(1＋a2)x]＝0，
解得x1＝0，x2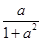＝，∴I＝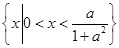
，∴I的长度为x2－x1＝.
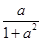(2)k∈(0，1)，则0<1－k≤a≤1＋k<2.
由(1)知I的长度为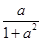，设g(a)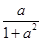＝，令g′(a)＝
>0，则0<a<1.
故g(a)关于a在[1－k，1)上单调递增，在(1，1＋k]上单调递减．
g(1－k)＝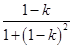
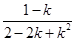＝，g(1＋k)＝
，
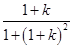故g(a)min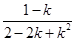＝，即I的长度的最小值为