问题
解答题
设函数f(x)是定义在(-1,1)上的偶函数,在(0,1)上是增函数,若f(a-2)-f(4-a2)<0,求实数a的取值范围.
答案
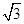 <a<
<a<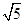 且a≠2.
且a≠2.
由f(x)的定义域是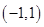 ,知
,知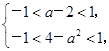 解得
解得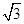 <a<
<a<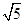 .
.
由f(a-2)-f(4-a2)<0,得f(a-2)<f(4-a2).
因为函数f(x)是偶函数,所以f(|a-2|)<f(|4-a2|).
由于f(x)在(0,1)上是增函数,所以|a-2|<|4-a2|,解得a<-3或a>-1且a≠2.
综上,实数a的取值范围是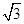 <a<
<a<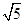 且a≠2.
且a≠2.
