已知奇函数 f (x) 在 (-¥,0)∪(0,+¥) 上有意义,且在 (0,+¥) 上是增函数,f (1) = 0,又函数 g(q) = sin 2q+ m cos q-2m,若集合M =" {m" | g(q) < 0},集合 N =" {m" | f [g(q)] < 0},求M∩N.
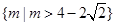 .
.
题目分析:根据条件中 是奇函数的这一条件可以求得使
是奇函数的这一条件可以求得使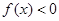 的
的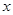 的范围,再根据
的范围,再根据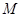 与
与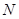 的表达式,可以得到
的表达式,可以得到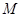 与
与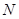 的交集即是使
的交集即是使 恒成立的所有
恒成立的所有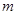 的全体,通过参变分离可以将问题转化为求使
的全体,通过参变分离可以将问题转化为求使 恒成立的
恒成立的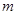 的取值范围,通过求函数最大值,进而可以求出
的取值范围,通过求函数最大值,进而可以求出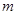 的范围.
的范围.
依题意,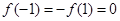 ,又
,又 在
在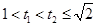 上是增函数,
上是增函数,
∴ 在
在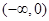 上也是增函数, 1分
上也是增函数, 1分
∴ 由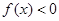 得
得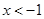 或
或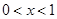 2分
2分
∴ 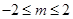 或
或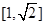 3分
3分
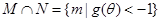 4分
4分
由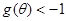 得
得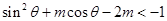 5分
5分
即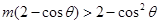 6分
6分
∴ 7分
7分
设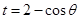 ,
, 9分
9分
∵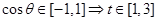 , 10分
, 10分
∴ , 11分
, 11分
且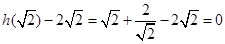 12分
12分
∴ 的最大值为
的最大值为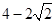 13分
13分
∴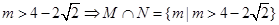 14分
14分
另解:本题也可用下面解法:
1. 用单调性定义证明单调性
∵对任意 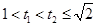 ,
,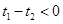 ,
,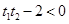 ,
,
∴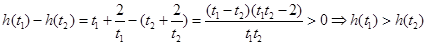 ,
,
即 在
在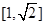 上为减函数,
上为减函数,
同理 在
在 上为增函数,得
上为增函数,得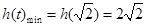 5分
5分
∴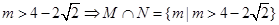 .
.
2. 二次函数最值讨论
解:依题意,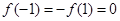 ,又
,又 在
在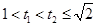 上是增函数,
上是增函数,
∴ 在
在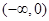 上也是增函数,
上也是增函数,
∴由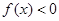 得
得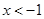 或
或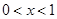
∴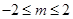 或
或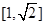 ,
,
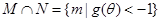 4分
4分
由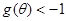 得
得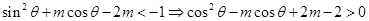 恒成立,
恒成立,
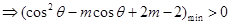 5分
5分
设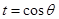 ,
,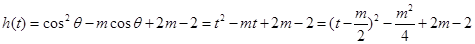 6分
6分
∵ ,
, 的对称轴为
的对称轴为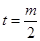 7分
7分
1°当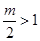 ,即
,即 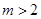 时,
时, 在
在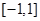 为减函数,∴
为减函数,∴ 9分
9分
2°当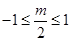 ,即
,即 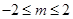 时,
时,
∴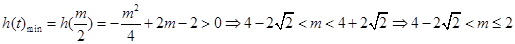 11分
11分
3°当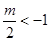 ,即
,即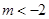 时,
时, 在
在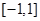 为增函数,
为增函数,
∴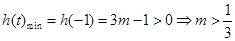 无解 13分
无解 13分
综上,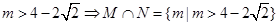 14分
14分
3. 二次方程根的分布
解:依题意,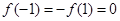 ,又
,又 在
在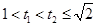 上是增函数,
上是增函数,
∴ 在
在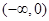 上也是增函数,
上也是增函数,
∴ 由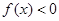 得
得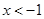 或
或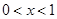
∴ 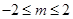 或
或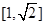 ,
,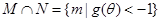 ,
,
由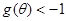 得
得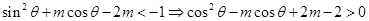 恒成立,
恒成立,
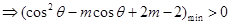 ,
,
设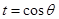 ,
,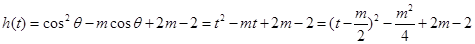
∵ ,
, 的对称轴为
的对称轴为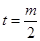 ,
,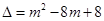 , 7分
, 7分
1°当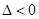 ,即
,即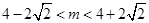 时,
时, 恒成立。 9分
恒成立。 9分
2°当 ,即
,即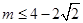 或
或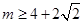 时,
时,
由 在
在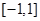 上恒成立
上恒成立
∴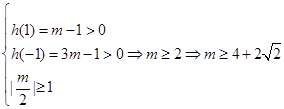 13分
13分
综上,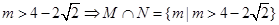 14分
14分
4.用均值不等式(下学段不等式内容)
∵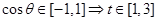 ,∴
,∴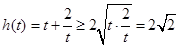 ,
,
且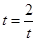 ,即
,即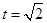 时等号成立。
时等号成立。
∴ 的最大值为
的最大值为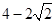 .
.
∴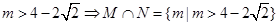 . 5分
. 5分
