问题
解答题
已知函数f(x)=loga(a-ax)(a>1)。
(1)求f(x)的定义域、值域;
(2)判断f(x)的单调性,并给出证明。
答案
解:(1)由a-ax>0,得ax<a,
∵函数y= ax (a>1)为增函数,
∴x<1,
又∵ax>0,
∴0<ax<a,
∴f(x)=loga(a-ax)<1,
故函数f(x)的定义域为(-∞,1),值域为(-∞,1)。
(2)f(x)为减函数。
证明:设x1<x2<1,则
f(x1)- f(x2)=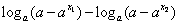 ,
,
∵x1<x2<1,a>1,
∴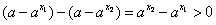 ,
,
∴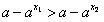 ,即
,即 ,
,
∴f(x1)- f(x2) >0,
∴f(x1)>f(x2),
∴函数f(x)在定义域(-∞,1)上为减函数。
