问题
计算题
（10分）如图所示，两个质量相等的弹性小球A和B分别挂在L1=0.81m，L2=0.36m的细线上，两球重心等高且互相接触，现将A球拉离平衡位置与竖直方向夹角小于5°后由静止开始释放，已知当A与B相碰时发生速度交换，即碰后A球速度为零，B球速度等于A球碰前的速度；当B与A相碰时遵循相同的规律，且碰撞时间极短忽略不计。求从释放小球A开始到两球发生第3次碰撞的时间t。（已知π2≈g）
答案
1.95s
两质量相等的弹性小球做弹性正碰时，两球速度交换。
由单摆周期公式有 TA=2π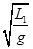
=1.8s （2分）
TB=2π
=1.2s （2分）
从释放小球A到第1次相碰经历时间 t1=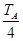 
=0.45s （1分）
从小球B摆起到第2次相碰经历时间 t2= 
=0.6s （1分）
从小球A摆起到第3次相碰经历时间 t3=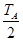 
=0.9s （1分）
所以从释放小球A到A、B第3次碰撞，共需时间 t=t1+t2+t3=1.95s （3分）
本题考查单摆的周期公式，由于两个小球为完全相同的弹性小球，碰撞类型为完全弹性碰撞，碰撞后互换速度，由单摆的振动周期公式可求解