问题
填空题
在平面直角坐标系xOy中,圆C的方程为(x-1)2+y2=4,P为圆C上一点.若存在一个定圆M,过P作圆M的两条切线PA,PB,切点分别为A,B,当P在圆C上运动时,使得∠APB恒为60°,则圆M的方程为 .
答案
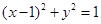
题目分析:根据题意利用直线与圆的关系,在直角三角形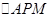 中,由
中,由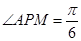 结合勾股定理可得:
结合勾股定理可得: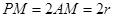 ,联想圆的定义知:点M和点C重合,又
,联想圆的定义知:点M和点C重合,又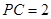 ,则
,则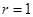 ,故圆M:
,故圆M: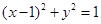 .
.
在平面直角坐标系xOy中,圆C的方程为(x-1)2+y2=4,P为圆C上一点.若存在一个定圆M,过P作圆M的两条切线PA,PB,切点分别为A,B,当P在圆C上运动时,使得∠APB恒为60°,则圆M的方程为 .
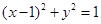
题目分析:根据题意利用直线与圆的关系,在直角三角形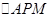 中,由
中,由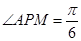 结合勾股定理可得:
结合勾股定理可得: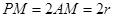 ,联想圆的定义知:点M和点C重合,又
,联想圆的定义知:点M和点C重合,又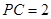 ,则
,则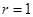 ,故圆M:
,故圆M: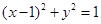 .
.