问题
解答题
函数f(x)＝2x2－2ax＋3在区间[－1，1]上最小值记为g(a)．
(1)求g(a)的函数表达式；
(2)求g(a)的最大值．
答案
（1）g(a)＝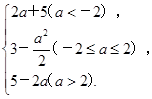
（2）g(a)max＝3
(1)①当a<－2时，函数f(x)的对称轴x＝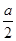
<－1，则g(a)＝f(－1)＝2a＋5；②当－2≤a≤2时，函数f(x)的对称轴x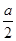＝∈[－1，1]，则g(a)＝f
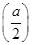＝3－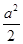
；③当a>2时，函数f(x)的对称轴x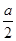＝>1，则g(a)＝f(1)＝5－2a.
综上所述，g(a)＝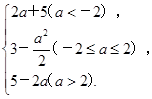
(2)①当a<－2时，g(a)<1；②当－2≤a≤2时，g(a)∈[1，3]；③当a>2时，g(a)<1.
由①②③可得g(a)max＝3.