问题
解答题
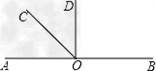
如图所示，O是直线AB上一点，∠AOC=
∠BOC，OC是∠AOD的平分线．
（1）求∠COD的度数．
（2）判断OD与AB的位置关系，并说出理由．
答案
解：（1）∵∠AOC+∠BOC=180°，∠AOC=
∠BOC，
∴
∠BOC+∠BOC=180°，解得∠BOC=135°，
∴∠AOC=180°﹣∠BOC=180°﹣135°=45°，
∵OC平分∠AOD，
∴∠COD=∠AOC=45°．
（2）OD⊥AB．
理由：由（1）知∠AOC=∠COD=45°，
∴∠AOD=∠AC+∠COD=90°，
∴OD⊥AB（垂直定义）．