解：（1）设2x+1=t，由于函数y=f（t）的定义域为[1，2]，故1≤t≤2，即1≤2x+1≤2，解得0≤x≤，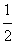

所以函数y=f（2x+1）的定义域为；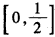

（2）设2x+1=t，因为1≤x≤2，所以3≤2x+1≤5，即3≤t≤5，函数y=f（t）的定义域为[3，5]

由此得函数y=f（x）的定义域为[3，5]；

（3）因为函数y=f（2x+1）的定义域为[1，2]，即1≤x≤2，所以3≤2x+1≤5，

所以函数y=f（x）的定义域为[3，5]，

由3≤2x-1≤5，得2≤x≤3，

所以函数y=f（2x-1）的定义域为[2，3]。