问题
解答题
过原点O作圆x2+y2-8x=0的弦OA。
(1)求弦OA中点M的轨迹方程；
(2)延长OA到N，使|OA|=|AN|，求N点的轨迹方程.
答案
(1)x2+y2-4x="0;" (2)x2+y2-16x=0
题目分析：（1）设M点坐标为（x，y），那么A点坐标是（2x，2y），
A点坐标满足圆x2+y2-8x=0的方程，所以， （2x）2+（2y）2-16x=0，
化简得M 点轨迹方程为x2+y2-4x=0．
（2）设N点坐标为（x，y），那么A点坐标是（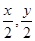
），
A点坐标满足圆x2+y2-8x=0的方程，
得到：（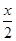
）2+（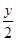
）2-4x=0，
N点轨迹方程为：x2+y2-16x=0。
点评：中档题，本题利用“相关点法”（“代入法”），较方便的使问题得解。