问题
解答题
求圆心在抛物线x2＝4y上，且与直线x＋2y＋1＝0相切的面积最小的圆
的方程．
答案
(x＋1)2＋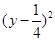
＝
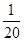
设圆心坐标为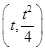
，半径为r.
根据已知得r＝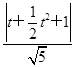
＝
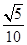(t2＋2t＋2)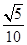＝ [(t＋1)2＋1]≥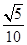，当t＝－1时取等号，此时r最小为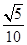，圆心坐标为(－1，
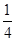)，故所求的圆的方程是(x＋1)2＋＝.
搜题请搜索小程序“爱下问搜题”
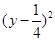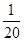求圆心在抛物线x2＝4y上，且与直线x＋2y＋1＝0相切的面积最小的圆
的方程．
(x＋1)2＋＝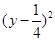
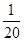
设圆心坐标为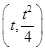，半径为r.
根据已知得r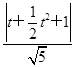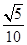＝＝ (t2＋2t＋2)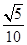＝ [(t＋1)2＋1]≥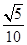，当t＝－1时取等号，此时r最小为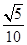，圆心坐标为(－1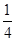，)，故所求的圆的方程是(x＋1)2＋＝.
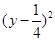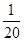阅读下面的节选诗句，回答问题。
| ||
| 1．哪几句诗写的是解放区的景象？作者在选取形象和选用词语上有什么特点？ ____________________________________________________________ 2．诗人是如何运用对比手法的？这样写有什么作用？ ____________________________________________________________ 3．这首诗是怎样将众多的形象贯穿组织成一个有机的整体的？ ____________________________________________________________ 4．把抽象的情感寄寓在具体的形象上，可使其具有可感性。请借鉴这种写法，写几句富有诗意的话，抒发自己的一种感情。 ____________________________________________________________ |