问题
解答题
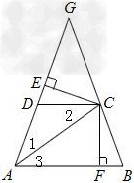
已知:如图,四边形ABCD中,AB∥CD,∠1=∠2,CD=CB,AD、BC的延长线相交于点G,CE⊥AG,垂足为E,CF⊥AB,垂足为F.
(1)请写出图中两组相等的线段(已知相等的线段除外);
(2)选择(1)中你所写的一组相等的线段,说出相等的理由.
答案
(1)解:CE=CF;DE=BF;
(2)求证:CE=CF.证明如下:
∵AB∥CD,
∴∠2= ∠3,
∵∠1=∠2,
∴∠1=∠3,
∴AC为∠DAB的平分线.
又∵CE⊥AG,CF⊥AB,
∴CE=CF.
