问题
解答题
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:f(ab)=af(b)+bf(a)。(1)求f(0)及f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)若f(2)=2,un=f(2n)(n∈N*),求证un+1>un(n∈N)。
答案
解:(1)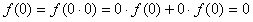
因为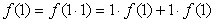 ,
,
所以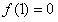 。
。
(2)f(x)是奇函数。
证明:因为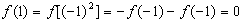 ,
,
所以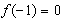
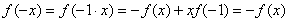
因此,f(x)为奇函数。
(3)证明:先用数学归纳法证明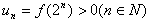
(i)当n=1时,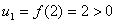 ;
;
(ii)假设当n=k时,
那么当n=k+1时,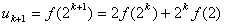
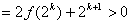
由以上两步可知,对任意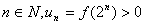
因为
所以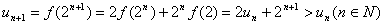 。
。
