问题
填空题
设抛物线y2=2px在与直线y=x交点处的曲率半径
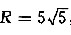 ,则此抛物线在该点处的切线方程是______.
,则此抛物线在该点处的切线方程是______.
答案
参考答案:x-2y+2=0
解析:
[分析]: 由Y2=2px知,当y=X时,X=Y=2p,且[*][*]
该曲线在(2p,2p)处的曲率半径为
[*]
抛物线方程为y2=2x,与y=x交点为(2,2),这时[*],该点处的切线方程为x-2y+2=0
设抛物线y2=2px在与直线y=x交点处的曲率半径
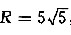 ,则此抛物线在该点处的切线方程是______.
,则此抛物线在该点处的切线方程是______.
参考答案:x-2y+2=0
解析:
[分析]: 由Y2=2px知,当y=X时,X=Y=2p,且[*][*]
该曲线在(2p,2p)处的曲率半径为
[*]
抛物线方程为y2=2x,与y=x交点为(2,2),这时[*],该点处的切线方程为x-2y+2=0