问题
解答题
已知圆方程:x2+y2﹣2ax+2y+a+1=0,求圆心到直线ax+y﹣a2=0的距离的取值范围.
答案
解:将圆方程配方得(x﹣a)2+(y+1)2=a2﹣a
故满足 a2﹣a>0,解得a>1或a<0
由方程得圆心(a,﹣1)到直线ax+y-a2=0的距离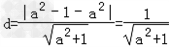 ,
,
当a>1时, ,得
,得 ;
;
当a<0,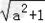 >1,0<d<1.
>1,0<d<1.
所以圆心到直线ax+y﹣a2=0的距离的取值范围为:
已知圆方程:x2+y2﹣2ax+2y+a+1=0,求圆心到直线ax+y﹣a2=0的距离的取值范围.
解:将圆方程配方得(x﹣a)2+(y+1)2=a2﹣a
故满足 a2﹣a>0,解得a>1或a<0
由方程得圆心(a,﹣1)到直线ax+y-a2=0的距离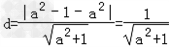 ,
,
当a>1时, ,得
,得 ;
;
当a<0,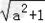 >1,0<d<1.
>1,0<d<1.
所以圆心到直线ax+y﹣a2=0的距离的取值范围为: