问题
解答题
某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m2与3m2.用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个.问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
答案
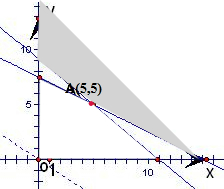
设A种原料为x个,B种原料为y个,
由题意有:
,3x+6y≥45 5x+6y≥55 x≥0 y≥0
目标函数为Z=2x+3y,
由线性规划知:使目标函数最小的解为(5,5),
即A、B两种原料各取5,5块可保证完成任务,且使总的用料(面积)最小.