问题
问答题
设f(x)在x0点可导，αn，βn为趋于零的正项数列，求极限
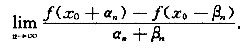
答案
参考答案：由于f(x)在点x0处可导，则
f(x0+△x)=f(x0)+f’(x0)△x+γ·△x
其中[*]，从而有
f(x0+αn)=f(x0)+f’(x0)αn+γ1·αn
f(x0-βn)=f(x0)+f’(x0)βn+γ2·βn
则
[*]
搜题请搜索小程序“爱下问搜题”
设f(x)在x0点可导，αn，βn为趋于零的正项数列，求极限
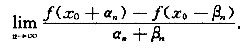
参考答案：由于f(x)在点x0处可导，则
f(x0+△x)=f(x0)+f’(x0)△x+γ·△x
其中[*]，从而有
f(x0+αn)=f(x0)+f’(x0)αn+γ1·αn
f(x0-βn)=f(x0)+f’(x0)βn+γ2·βn
则
[*]