问题
解答题
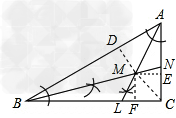
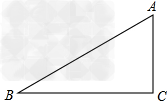
如图，在△ABC中，AB=20，AC=12，BC=16．试问在△ABC内能否找到一点，使这点到各边的距离相等？如果能，请用尺规作图法作出这一点，再证明，并求出这个距离；如果不能．请说明理由。
答案
解：能，作∠ABC和∠BAC的平分线，其交点为M，则点M到各边的距离相等；理由如下：作MD⊥AB，ME⊥AC，MF⊥BC，垂足分别为D，E，F，
∵BM是∠ABC的平分线，AM是∠BAC的平分线，
∴MD=MF，MD=ME（角的平分线上的点到这个角的两边的距离相等）
即MD=MF=ME．
连接CM，设MD=MF=ME=x，
在△ABC中，
∵AB=20，AC=12，BC=16，
而122+162=144+256=400=202，
即AC2+BC2=AB2，
则△ABC是直角三角形，且∠C=90°，
∴
，
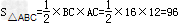又S△ABC=S△ABM+S△BCM+S△ACM
=
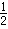（AB+BC+AC）x
=
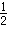×48x=24x，
则24x=96，x=4，
∴这个距离为4。
