问题
解答题
在△ABC中,CE⊥AB于E,在△ABC外作△ACD,使∠CAD=∠CAB,且DC=BC,过C作CF⊥AD,交AD的延长线于F.
(1)说明CE=CF的理由;
(2)说明BE=DF的理由.
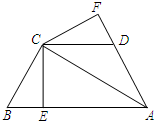
答案
证明:(1)∵∠CAD=∠CAB,CE⊥AB,CF⊥AD,
∴CE=CF;
(2)∵CE⊥AB,CF⊥AD,
∴∠CEB=∠F=90°,
在Rt△CBE和Rt△CDF中,
,CB=CD CE=CF
∴Rt△CBE≌Rt△CDF(HL),
∴BE=DF.
