问题
选择题
函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<
|
答案
由于函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<
)的最小正周期为π,故π 2
=π,ω=2.2π ω
把其图象向右平移
个单位后得到的函数的解析式为 y=sin[2(x-π 12
)+ϕ]=sin(2x-π 12
+ϕ),为奇函数,π 6
∴-
+ϕ=kπ,∴ϕ=kπ+π 6
,k∈z∴ϕ=π 6
,∴函数f(x)=sin(2x+π 6
).π 6
令2x+
=kπ,k∈z,可得 x=π 6
-kπ 2
,k∈z,故函数的对称中心为( π 12
-kπ 2
,0),k∈z,π 12
故点(
,0)是函数的一个对称中心,5π 12
故选C.

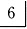 缺失,可摘局部义齿修复,基牙
缺失,可摘局部义齿修复,基牙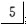 靠近缺隙侧倒凹大,这种情况下,上可设计()
靠近缺隙侧倒凹大,这种情况下,上可设计()