问题
解答题
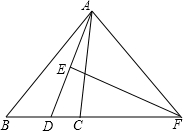
如图，AD平分∠BAC，EF垂直平分AD交BC的延长线于F，连接AF．求证：∠B=∠CAF．
答案
证明：∵EF垂直平分AD，∴AF=DF，∠ADF=∠DAF，
∵∠ADF=∠B+∠BAD，
∠DAF=∠CAF+∠CAD，
又∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠B=∠CAF．
搜题请搜索小程序“爱下问搜题”
如图，AD平分∠BAC，EF垂直平分AD交BC的延长线于F，连接AF．求证：∠B=∠CAF．
证明：∵EF垂直平分AD，∴AF=DF，∠ADF=∠DAF，
∵∠ADF=∠B+∠BAD，
∠DAF=∠CAF+∠CAD，
又∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠B=∠CAF．
