问题
证明题
已知在△ABC中，∠C=90°，CD⊥AB于D，设BC=a，AC=b，AB=c，CD=h。
求证：（1）c+h>a+b；
（2）以a+b、h、c+h为边的三角形是直角三角形。
答案
证明：（1）∵S△ABC=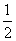
ab=
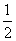ch
∴ab=ch
∵(c+h)2=c2+2ch+h2
(a+b)2=a2+b2+2ab=c2+2ch
∴(c+h)2>(a+b)2
∴c+h>a+b
（2）由（1）得：(a+b)2+h2=(c+h)2
∴a+b，h，c+h组成的三角形为直角三角形。